MST
Minimum Spanning Tree
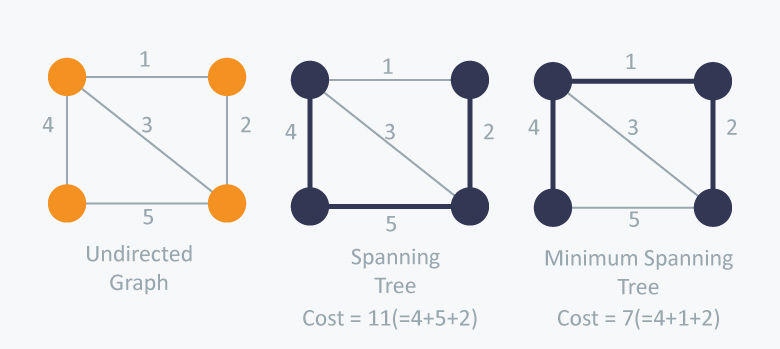
What is spanning tree?
Graph is weighted undirected and find a tree which has lowest weights.
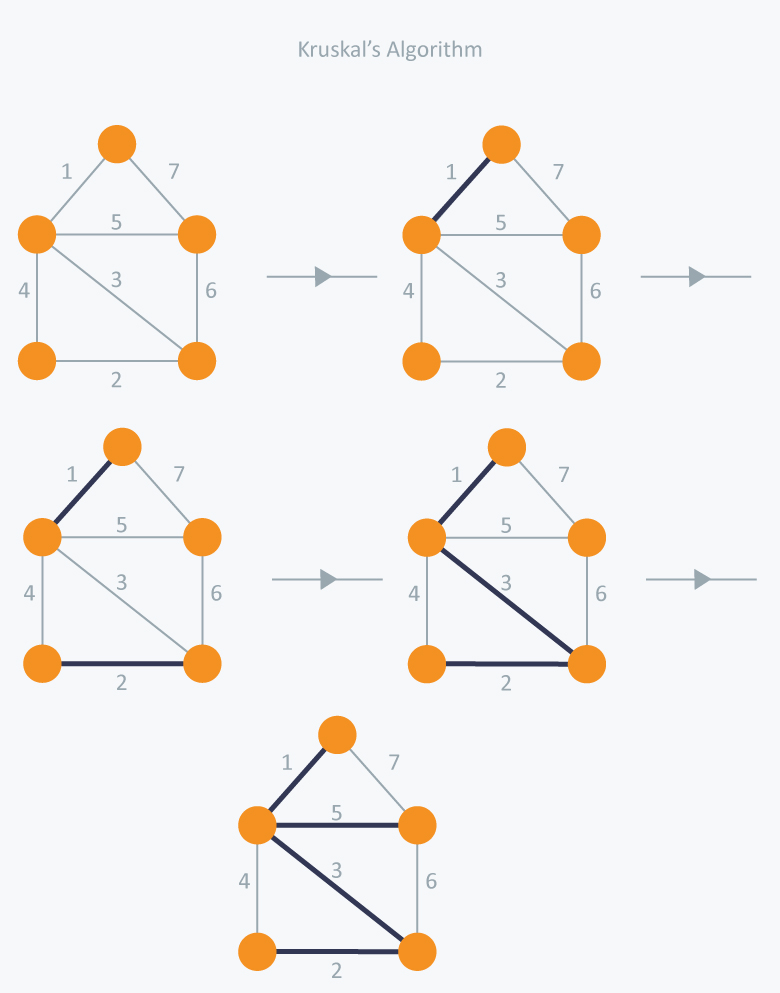
Kruskal’s Algorithm
1. Sort edges of graph with their weights.
2. Take edge and check whether it makes cycle or not.
3. If it doesn't make cycle than take this edge in MST.
4. else not take this edge in cycle.
5. apply 2,3,4 until all edges are taken.
For checking adding edge makes cycle or not we make DFS( see my previous post) but it takes O(V+E) time it is expensive, so use DSU.
DSU algorithm:-
Below example are explain algorithm.
1. first declare Arr[i]=i.
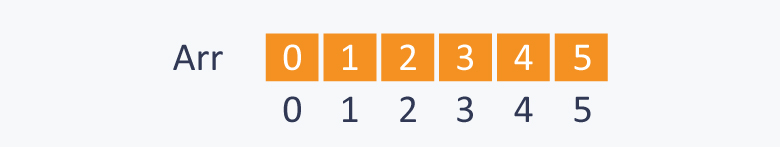
2. make size[i]=i.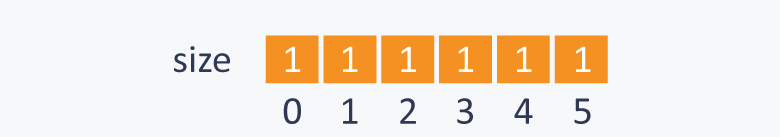
3.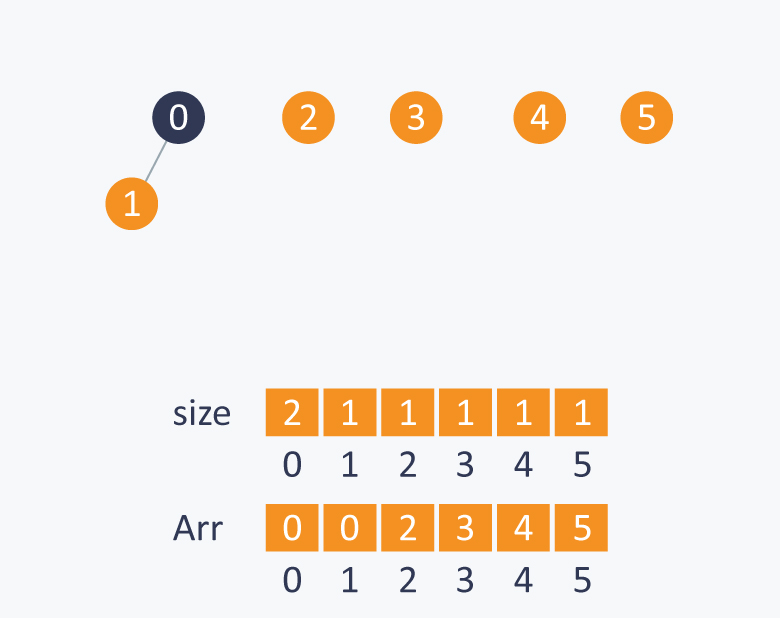
4.
Connect to 2 to 0 because size[0]> size[1].
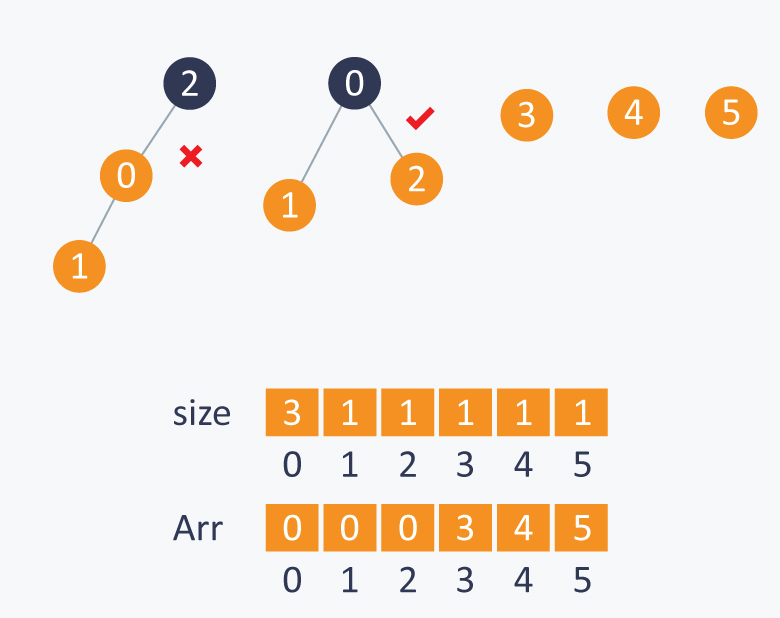
DSU algorithm:-
Below example are explain algorithm.
1. first declare Arr[i]=i.
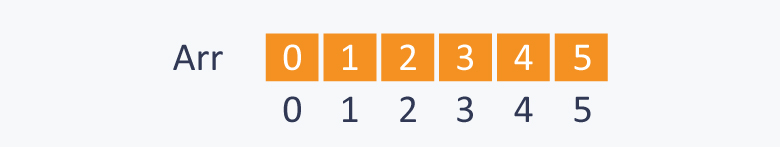
2. make size[i]=i.
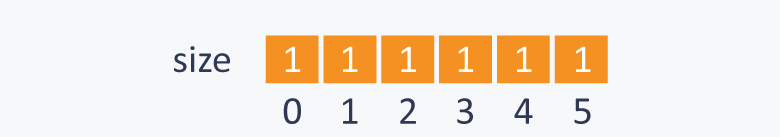
3.

4.
Connect to 2 to 0 because size[0]> size[1].

My DSU code:-
class DSU { int par[], size[], connectedComponent; DSU(int n) { par = new int[n]; size = new int[n]; for (int i = 0; i < n; i++) { size[i] = 1; par[i] = i; } connectedComponent = n; } int root(int n) { if (n == par[n]) return n; return par[n] = root(par[n]); } boolean union(int u, int v) { return f_union(root(u), root(v)); } boolean f_union(int u, int v) { if (u == v) return false; if (size[u] > size[v]) { size[u] += size[v]; par[v] = u; } else { size[v] += size[u]; par[u] = v; } connectedComponent--; return true; } DSU clone_DSU() { DSU t = new DSU(par.length); t.connectedComponent = connectedComponent; for (int i = 0; i < par.length; i++) { t.par[i] = par[i]; t.size[i] = size[i]; } return t; } }
code for MST:-
class Kruskal_Algorithm{ //edge[0]--> from //edge[1]--> to //edge[2]--> weight int GIVE_MST(ArrayList<Integer> Graph[],int numberOfNodes,int numersOfEdges,int Edgs[][]){ Arrays.sort(Edgs, new Comparator<int[]>() { @Override public int compare(int[] o1, int[] o2) { return Integer.compare(o1[2],o2[2]); } }); DSU dsu=new DSU(numberOfNodes); int ans=0; for (int i = 0; i <numersOfEdges ; i++) { if(dsu.union(Edgs[i][0],Edgs[i][1])){ ans+=Edgs[i][2]; } } return ans; } }reference:all my images are taken from https://www.hackerearth.com
Comments
Post a Comment