introduction to Graph

Graph Algorithm

Graphs are mathematical structures that represent pairwise relationships between objects. 

There two things to represent graph.

1) Node:Nodes are entities whose relationships are expressed using edges.

2) Edge: Edges are the components that are used to represent the relationships between various nodes in a graph.

Types of graphs

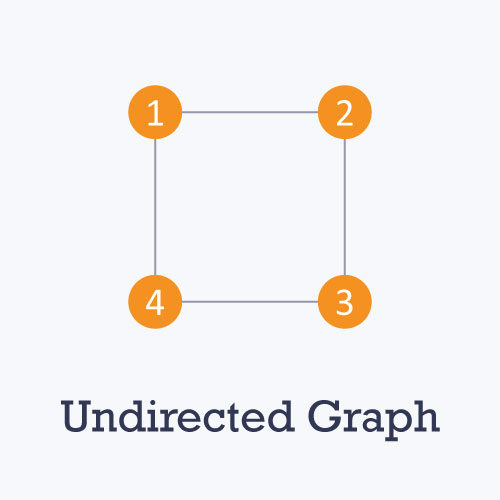
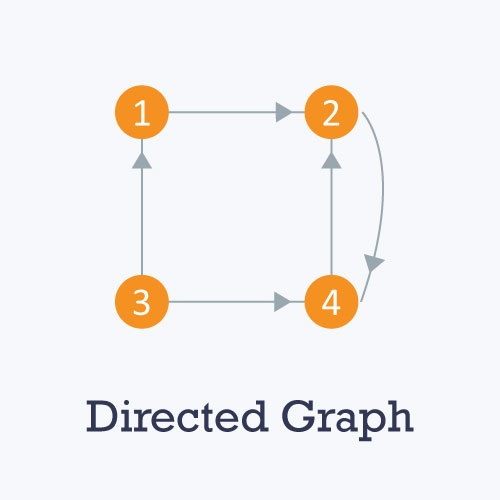
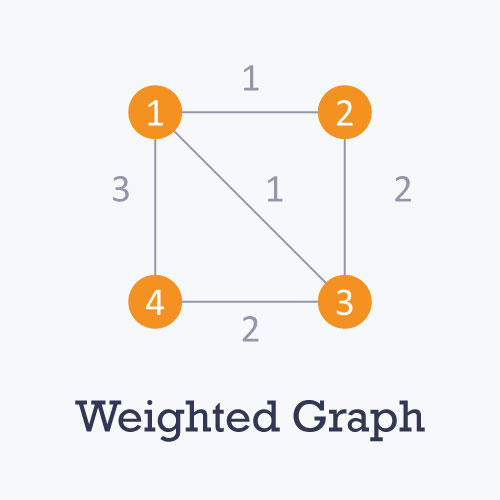
Graph representation

You can represent a graph in many ways. The two most common ways of representing a graph is as follows:

Adjacency matrix

An adjacency matrix is a VxV binary matrix A. Element $A_{i,j}$ is 1 if there is an edge from vertex i to vertex j else $A_{i,j}$ is 0.

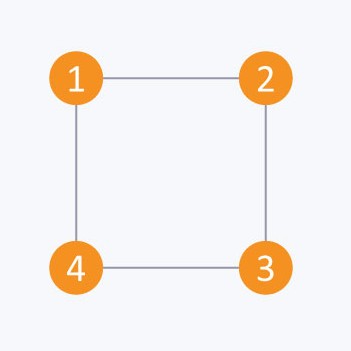
The adjacency matrix of the following graph is:
i/j : 1  2   3   4
1 : 0 - 1 - 0 - 1
2 : 1 - 0 - 1 - 0
3 : 0 - 1 - 0 - 1
4 : 1 - 0 - 1 - 0

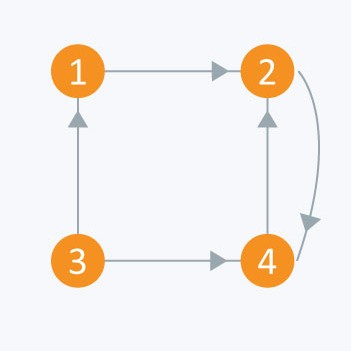
The adjacency matrix of the following graph is:

i/j: 1   2   3   4
1 : 0 - 1 - 0 - 0
2 : 0 - 0 - 0 - 1
3 : 1 - 0 - 0 - 1
4 : 0 - 1 - 0 - 0

Code:-

public void run() {
    InputReader sc = new InputReader(System.in);
    // Scanner sc=new Scanner(System.in);    //  Random sc=new Random();    PrintWriter out = new PrintWriter(System.out);

    int numberOfNodes=sc.nextInt();
    int graph[][]=new ArrayList[numberOfNodes][numberOfNodes];

    int numberOfEdges=sc.nextInt();
    for (int i = 0; i <numberOfEdges ; i++) {
        int u=sc.nextInt();
        int v=sc.nextInt();
        graph[u][v]=1;
        graph[v][u]=1;
    }

    out.close();
}

Disadvantage:

       It takes more memory. O(n^2).

Adjacency list

     you should use list instead of matrix.

E.g.

N1 → 2
N2 → 4
N3 → 1 → 4
N4 → 2

My code :-

public void run() {
    InputReader sc = new InputReader(System.in);
    // Scanner sc=new Scanner(System.in);    //  Random sc=new Random();    PrintWriter out = new PrintWriter(System.out);

    int numberOfNodes=sc.nextInt();
    ArrayList<Integer> graph[]=new ArrayList[numberOfNodes];
    for (int i = 0; i <numberOfNodes ; i++) {
        graph[i]=new ArrayList<>();
    }
    int numberOfEdges=sc.nextInt();
    for (int i = 0; i <numberOfEdges ; i++) {
        int u=sc.nextInt();
        int v=sc.nextInt();
        graph[u].add(v);
        graph[v].add(u);
    }

    out.close();
}

Advantage:

       It takes less memory. O(V+E).